The type of kiln hood assembly can affect kiln operation significantly. Computational fluid dynamics modelling on four different types of kiln hood assemblies in a full-scale cement kiln has shown that clinker bed temperatures can show differences of up to 200˚C.
The burner is responsible for providing the thermal energy needed for the clinkerisation process to take place inside a cement kiln. It can burn several types of fuel: from petcoke and oil to biomass. Despite presenting issues in terms of safe storage and handling, solid fuels are more efficient than gas and oil. When gas is replaced by coal, kiln production reportedly increases by 2-3 per cent. This improvement is mainly related to the higher emissivity of the coal flame, as radiation is the main mechanism of heat transfer inside the kiln. Coal flame emissivity is around 0.85, while oil and gas flame emissivities are about 0.5 and 0.3, respectively. It is also known that the radiation from a flame is mainly due to coal/petcoke particles and fly ash suspended in the flow, as well as from the soot formed in the burning process.
“CFD solves fluid flow problems through numerical methods and algorithms.4 It is a powerful tool that is used in many fields of engineering because it reduces the time needed for projecting an equipment or to tackle an issue, consequently lowering costs.”
The results of computational fluid dynamics (CFD) for the combustion of petcoke in a full-scale cement kiln and the effects of hood assembly on kiln operation are presented below. The software used in the simulations is the ANSYS Fluent v16.1. Geometry, mesh, mathematical models and boundary conditions for the problem simulations are shown. Temperature and velocity profiles inside the kiln, including the near region of the burner, as well as coal particle trajectories, are discussed and compared for four distinct hood assemblies.
Computational fluid dynamics
CFD solves fluid flow problems through numerical methods and algorithms. It is a powerful tool that is used in many fields of engineering because it reduces the time needed for projecting an equipment or to tackle an issue, consequently lowering costs. The transport equations expressing the conservation principle (such as mass, momentum and energy equations, etc) all have the same form, making resolution simpler when compared to other methods.
The general form is presented below in tensor notation and cartesian coordinates:
where:
Φ = dependent variable
ui = velocity

component in the i direction
ρ = density
t = time.
The first term on the left of the equation is the transient term and denotes accumulation of Φ in the control volume. The second term on the left is the convective part, responding to the transport of Φ due to the velocity field. On the right, the diffusion term responds to the transport of Φ by its gradients, where Γ is diffusion coefficient of the fluid. SΦ is the source term and takes into account any source or sink that produces or dissipates Φ. Spare terms from transport equations adaptation to the general form of the previous equation, as well as terms from coordinates transformation, are also considered a source term. The control volume method 5 is employed to obtain the algebraic equations from the partial differential equations describing the physical problem. This method involves dividing the domain into control volumes so that every volume surrounds only one node. The set of equations is then numerically integrated over each volume in an iterative way.
Computational domain and mesh
The kiln and burner computational domains are shown in Figure 1. The kiln domain considers the first 30m of the kiln’s length (from burner tip to the domain outlet) and the full 3.6m of its diameter. The tertiary duct is 2.4m in diameter and only a short part of its length is modelled. Secondary air enters at the bottom of the hood, through a surface area of 18.5m2. The burner’s diameter is 0.566m. The total areas of primary air channels are:
• external: 2.65×10-3m2
• tangential: 1.49×10-3m2
• fuel transport: 9.66×10-3m2
• internal: 2.15×10-4m2.
The mesh generated has a total of nearly 2m polyhedral cells. Refinements were necessary close to the burner tip to more accurately capture the physical phenomena on this region.

Models and boundary conditions
For the gas phase, equations for mass, momentum, energy, species and turbulence are solved. The chosen turbulence model was the SST k-ω. Coal combustion is carried out through species transport with volumetric reactions, and the net reaction rate is taken as the minimum of Arrhenius expressions for chemical reactions and turbulent mixing between oxidant and fuel (finite rate/eddy dissipation model). To account for radiation heat transfer, which is the most important heat transfer mechanism inside the kiln, the P-1 model was chosen as it suits the problem well. The gas absorption coefficient is calculated using the weighted sum of grey gases model (WSGGM) and the scattering of gaseous combustion products is considered to be negligible once the scattering of coal particles is 2-3 orders of magnitude larger. This work does not take into account the heat transfer from the free board and walls to the clinker bed, and for that reason the temperature profile inside the entire kiln is slightly overestimated. The discrete phase model (DPM) is used to track coal particles, and a total of about 7500 parcels representing the whole flux of fuel injection is generated, making use of a random walking model (RWM) as a dispersion model. The particle surface reaction rate model is set as the kinetics/diffusion-limited as both mechanisms are important in the combustion of solid fuels. The proximate analysis of the petcoke shows a volatile content of 17 per cent, fixed carbon of 82 per cent and moisture content of one per cent. The coal particles are injected at 50˚C and at 30 m/s. The fuel flux is 3400kg/h. Particles participate in radiation and are actually responsible for a large part of flame radiation (around 80 per cent ). The particle emissivity and scattering factors are assumed to be respectively, 0.9 and 0.6. Kiln and burner walls are assumed to be adiabatic and are modelled as grey surfaces. Their emissivities are 0.8 for the kiln wall and burner body and 0.5 for the burner tip. Table 1 presents the boundary conditions for flux and temperature of primary, secondary and tertiary airs. Tangential primary air is injected at an angle of 30˚.

Hood assemblies
The previous discussion presented geometry, mesh and boundary conditions for the base case. The first variation on the hood geometry under study was the centralisation of the tertiary air duct. The next case considered a reduced surface area at the bottom of the hood for an air inlet of 15.4m2 compared to 18.5m2 in the original configuration. A third possibility for the hood assembly was protrusion of the burner into the kiln by half a metre. All other geometric parameters, as well as mesh, models and boundary conditions, were kept as set for the base case.
Results and discussion
Figure 2 shows the temperature from the entrance of kiln (considered as the burner side, where clinker is discharged) for all four cases studied. The temperature at the initial point of sampling is 1350K (1077˚C), slightly above injection temperature of air at inlet. In the first 1.5m in the axial direction, the temperature rises to 2100K (1827˚C) in the base case, 2050K (1777˚C) where a smaller area for air intake is considered.
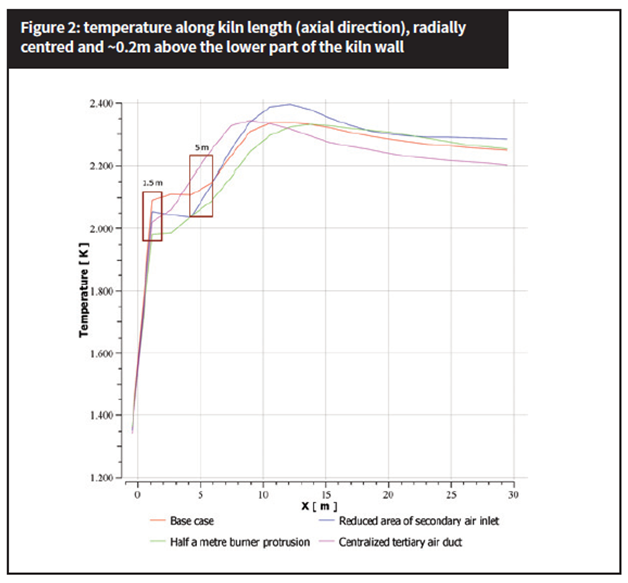
For protrusion of the burner it is below 2000K (1727˚C) and stays below 2050K (1777˚C) for the case with centralised tertiary duct. After 5m, the temperature is over 2100K (1827˚C) for base case and below 2100K (1827˚C) for the case with reduced air inlet area. For protrusion of the burner, it reaches 2050K (1777˚C), while with a centralised tertiary air duct it is 2200K (1927˚C). Between 5-10m there is a maximum difference of 200˚C among the cases, with the protrusion of the burner showing the lower temperature values, and the centralised tertiary air duct the higher values throughout most of this interval. From 10m onwards, a difference of 100˚C is maintained, with lower values for the centralised tertiary air duct and higher values for the reduced surface area for air inlet. As the air inlet is made through the bottom of the hood, a recirculating zone underneath the burner is common to all cases (see Figure 3). A small recirculation at the upper part of the kiln can also be seen in the centralised tertiary air duct scenario. In the case with reduced air inlet area, the recirculation zone gets closer to the burner tip. When the burner is repositioned further into the kiln, velocity vectors show a more centralised, symmetrical and fairly stable profile, holding higher velocities further down in axial direction.
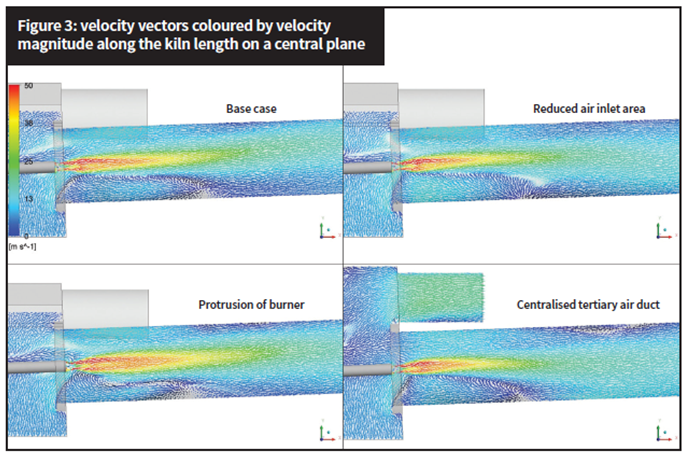
Figure 4 presents vectors on a cross-section 0.1 m behind the burner. For the case with a 0.5m protrusion of the burner inside the kiln, this plane cut is and therefore slightly ahead than in the other three cases, and that is why recirculation in this case seems to be much more pronounced. The case with reduced air inlet area does not greatly differ from the base case. On the other hand, when the tertiary air duct is placed in the centre of the hood, the velocity vectors and magnitude on this plane at the entrance of the kiln are the most uniform and symmetrical compared to all other cases. Figure 5 shows temperature profiles for all four cases. Due to the recirculation zone (seen in Figures 3 and 4), the gas temperature on these regions is higher compared to temperatures in the upper part of the kiln entrance, as can be visualised in Figure 5. High temperatures at these locations, ie, near the discharge region, should be carefully tracked once there is availability of O2, favouring therefore NOx formation.

In the case with reduced air inlet area, as recirculation reaches up to the vicinity of the burner tip, the temperature in this region is consequently greater than the base case. The same occurs with protrusion of the burner once the burner is inserted further into the kiln, being repositioned nearer the recirculation zone. Due to the recirculation presented at the upper part of the kiln, the temperature profile for the centralised tertiary air duct shows higher values at this location (see Figure 5 – bottom right and Figure 6 – bottom right).

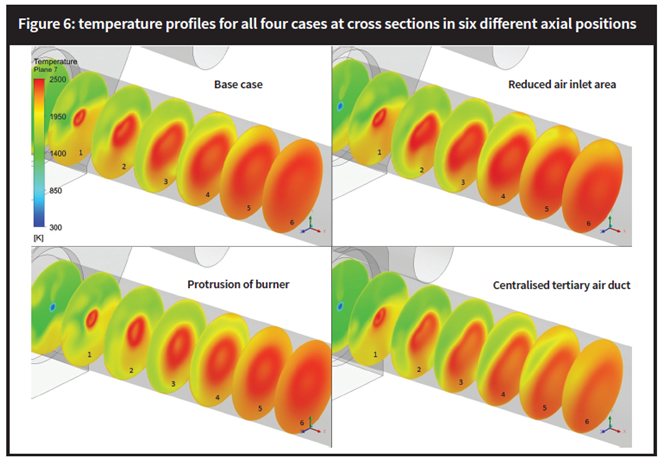
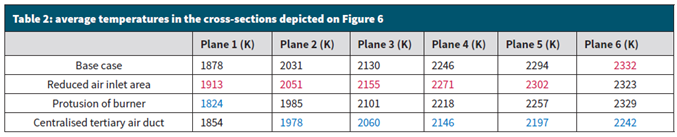
Figure 6 shows the temperature in six different cross-sections along the first 10m of the kiln’s length. Table 2 summarises the average temperature calculated at each plane, for every assembly analysed. The blue data are the lower values found amongst the different cases and the red data the highest values. The centralised tertiary air duct case shows the lower temperature averages, with a minimum difference of nearly 60˚C and a maximum difference of almost 125˚C when compared to the highest average values for temperature, found mostly to be in the case of the reduced inlet area for the secondary air. Differences of between 24˚C and 100˚C were found when comparing this case to the base case.
Of particular note is how uniform and symmetrically distributed the temperature profile is for the case with the protrusion of the burner in the kiln. Fuel particle tracks, coloured by residence time, are presented in Figures 7 and 8. With the reduced air inlet area and centralised tertiary air duct, residence times are slightly higher than in the base case and in the protrusion of the burner scenario. Seen from the domain outlet (Figure 8), particle tracks for the cases with reduced air inlet area and with centralised tertiary air duct present a little deflection to the right and downwards. This might be a consequence of both longer residence times and flow field characteristics, as it seems that for these two cases the vectors bend towards the lower part of the kiln wall. Moreover, greater residence times mean that the fuel burns more slowly, explaining the lower temperature averages for the centralised tertiary air duct case. The same uniformity seen on temperature and velocity profiles for the protrusion of the burner case is also seen with the fuel particle trajectories: particle paths are highly symmetrical and centred for the whole kiln length where burning takes place.Last but not least, the calculated total flux entrainment of secondary air into the fuel region, known to improve burner performance and described in detail in a previous article, are:
• base case – 1.339kg/s
• reduced air inlet area – 0.909kg/s
• protrusion of the burner – 1.364kg/s
• centralised tertiary air duct – 1.030kg/s.


Conclusions
A
CFD study of four different hood assemblies of a full-scale cement kiln has
been conducted. Modelling included the combustion of solid fuel particles and
radiation heat transfer. Results showed that temperature values in the clinker
bed region can present differences of up to 200˚C depending on the hood
assembly. Concerning the cases with reduced air inlet area and centralised
tertiary air duct, velocity vectors showed slightly deflected profiles, which
in turn affected the temperature and particle trajectory profiles. The case
with the protrusion of the burner seems to improve velocity, temperature and
particle tracks, as the results show a highly uniform and
symmetrically-distributed profiles for both continuous and disperse phases.
This case is also the one that allows more secondary air entrainment into the
fuel injection region.
REFERENCES
1 ALSOP, PA (2014) Cement Plant Operations Handbook. 6th edition. Dorking, UK: Tradeship Publications, 290p.
2 PERRY, RH AND GREEN, DW (1997) Perry’s Chemical Engineers’ Handbook. 7th edition. New York, USA: McGraw Hill Professional, 2640p.
3 HOTTEL, HC AND SAROFIM, AF (1967) Radiative Transfer. New York, USA: McGraw-Hill Book Company.
4 WHITE, FM (1991) Viscous Fluid Flow. 2nd Edition. New York, USA: McGraw-Hill Book Company, 614p.
5 PATANKAR, SV (1980) Numerical Heat Transfer and Fluid Flow. Boca Raton, USA: CRC Press, 214p.
6 FRIEDMAN, R (1998) Principles of Fire Protection Chemistry and Physics. 3rd edition. Quincy, USA: National Fire Protection Association, 296p.
7 RANADE, VV AND GUPTA, DF (2014) Computational Modeling of Pulverized Coal Fired Boilers. Boca Raton, USA: CRC Press, 271p.
8 BACKREEDY, RI, FLETCHER, LM, MA, L, POURKASHANIAN, M AND WILLIAMS, A (2006) ‘Modelling Pulverised Coal Combustion Using a Detailed Coal Combustion Model’ in: Combustion Science and Technology, 178, p763-787.
9 MASTORAKOS, E, MASSIAS, A, TSAKIROGLOU, CD, GOUSSIS, DA, BURGANOS, VN AND PAYATAKES, AC (1999) ‘CFD Predictions for Cement Kilns Including Flame Modelling, Heat Transfer and Clinker Chemistry’ in: Applied Mathematical Modelling, 23 (1), p55-76.
10 DANOV, D, PETKOV, V AND TSANEV, V (2007) ‘Investigations of Thermal Infrared Emissivity Spectra of Mineral and Rock Samples’ in: BOCHENEK, Z (ED) (2007) New Developments and Challenges in Remote Sensing. Rotterdam, The Netherlands: Millpress, p145-152.
11 JENKINS, B AND MULLINGER, P (2014) Industrial and Process Furnaces: Principles, Design and Operation. 2nd edition. Oxford, UK: Butterworth-Heinemann, 676p.
12 TOUIL, D, BELABED, HF, FRANCES, C AND BELAADI, S (2005) ‘Heat Exchange Modeling of a Grate Clinker Cooler and Entropy Production Analysis’ in: International Journal of Heat and Technology, 23, (1), p61-68.
13 MANICKAM, B, DINKELACKER, F AND LOBE, T AND TERTYCHNYY, M (2009) ‘Enriched Oxygen Combustion Simulation for Rotary Kiln Application’ in: Proceedings of the Fourth European Combustions Meeting, Vienna, Austria, 14-17 April.
14 INCROPERA, FP AND DEWITT, DP (1998) Fundamentals of Heat and Mass Transfer. 4th edition. Hoboken, USA: John Wiley & Sons Inc.
15 FAVALLI, RC, FABIANI, LF, DE PINHO, LF (2015) ‘Enhancing the Performance of Kiln Burners’ in: WC, November, p111-114.

